.
How do you get from there to a phase estimate for the protein,
T?
OK, you've collected your MAD data and run it through a phasing program
that has produced initial estimates for the three quantities
FT, FA, and
.
How do you get from there to a phase estimate for the protein,
T?
Since T =
A +
,
if you had a value for A
then you'd be all set. To get this you need to locate the anomalous
scattering atoms in the unit cell, so that you can calculate the phase
A of their contribution to
the total scattering. The simplest way to do this is through Patterson
analysis; it amounts to solving an n atom structure, where
n is the number of anomalous scattering atoms.
There are many possible Patterson maps you might calculate using the data
you've collected. Of these, the most familiar may be the
Bijvoet Difference Patterson
, calculated with coefficients
F
.
To increase the signal-to-noise ratio in your map you would logically choose
F values from whichever of your
wavelengths 
has the largest expected
difference in F+ and F-, i.e.
the one with the largest 
.
Here is a Harker section from such a map calculated using the anomalous
signal from a single Cu atom in the 96 residue metalloprotein CBP [Guss,
et al. 1989]:
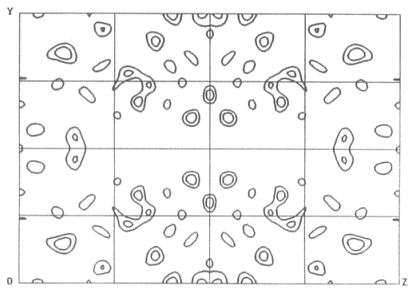
F from
peak = 1.3771Å
= 4.17e
As you can see, it's rather noisy.
That's because even at the optimal wavelength the maximal value of
is only 4.2e.
You can do much better than that, however. Rather than calculating any map
which uses only a subset of the data collected, you can instead use your
newly estimated value for |FA| to calculated a Patterson
map with coefficients
|FA|.
Because all of the data you collected contributes simultaneously to this
map, it will be less noisy than a map calculated using only a subset of the
data:
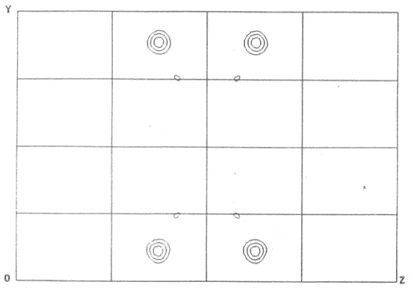
If there are many anomalous scattering atoms in your structure then it may be difficult to interpret the resulting Patterson maps. 20 anomalous scattering atoms is about the upper limit.
The most successful approach developed to date for locating larger numbers of anomalous scattering atoms is the 'dual space' method implemented in the programs shake-n-bake (Smith et al, 1998) and shelxd (Sheldrick, 1998; shelx home page). These programs alternate cycles of work in real space (Patterson interpretation and placement of trial atomic positions) and work in reciprocal space (tangent refinement). Both programs have been used successfully to locate more than 50 Se sites in a SeMet substituted protein.
back to index
next topic