MAD phasing - part 5

Bayesian estimates of |F_A|

One problem with the estimates for |FA| which come directly from the Karle/ Hendrickson equations is that the values are not always reasonable; e.g. sometimes the estimate for |FA| is greater than the total scattering power of the atoms involved. Terwilliger (1994) suggests correcting this by using a Bayesian estimate for |FA| predicated on the prior expected distribution of values:
P(F_A) exp(-F_A / ), where is the expected mean square value of F_A within a given resolution shell, given whatever we know about B values, scattering factors, etc.

Furthermore we can also use prior knowledge about the likely errors in our data to condition the probability of the observed quantities = 1/2(|F⁺| + |F^-|) and F = (|F⁺| - |F^-|).

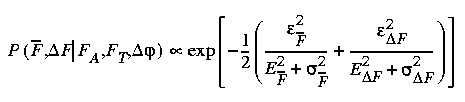
where

represents experimental uncertainty

E represents additional uncertainty

represents the difference between observed and calculated values of and F

After a bit more of this sort of analysis we arrive at the Bayesian estimate for any quantity <x> that depends on F_A, F_T, and :

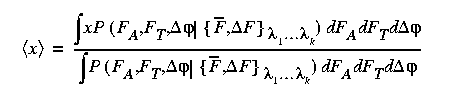
The integration should properly run over all three variables F_A, F_T, , but Terwilliger suggests taking F_T as being purely defined by its most probable value in order to save computational time.

back to index

next topic