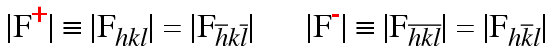
The members of a Friedel pair are related to each other by inversion through the origin, this symmetry operation is by definition not present in any non-centrosymmetric space group. However, each member of the pair may have true symmetry equivalents, for example 2-fold related reflections in space groups P2 or P21. These true symmetry equivalents of a Bragg reflection have equal amplitude even in the presence of anomalous scattering. So true symmetry equivalents of one member of a Friedel pair form a set all of whose members have the same amplitude |F+|, while all symmetry equivalents of the other member of the Friedel pair form a second set whose members share a different amplitude |F-|.
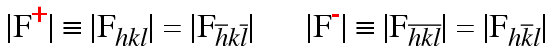
A Bijvoet pair contains one reflection from each of these two sets. The original Friedel pair is thus also a Bijvoet pair, but a Bijvoet pair is not necessarily a Friedel pair.
The difference in the measured amplitude for a Bijvoet pair is called a
Bijvoet difference, or 
F.
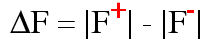
A Patterson map calculated with coefficients
F2
should contain only peaks corresponding to interatomic vectors between
pairs of anomalous scattering atoms. This is often the first step in
MAD phasing, since the location of the anomalous scattering atoms is
needed to develop MAD phase estimates.
If you have phase estimates for your structure, you can also use the
Bijvoet differences to calculate a Fourier map. The coefficients for
this map are
(F; 
+90°)
Note that the phases used in calculating the map are 90° different
from the phase estimates for the structure as a whole, since the
Bijvoet difference arise from the imaginary contribution to the total
scattering, 
.
Why can we use phase estimates for the structure as a whole,
rather than for the anomalous scattering atoms themselves?
Adding 90° to the phase is a very clever trick that gets around
this problem (Strahs and Kraut, 1968).
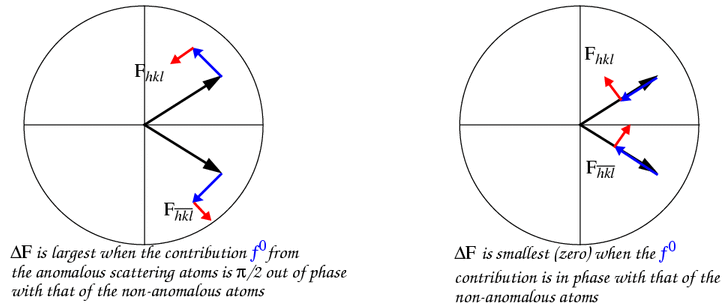
It works because F
is large exactly when the phase angle of 
for the anomalous scattering atoms happens to be ~90° away from that of the
rest of the structure (see figure). The reflections for which
+90° is a bad estimate are exactly the
reflections for which F is small and hence does
not contribute much to the map anyhow.
X-ray Anomalous Scattering
Choosing wavelengths for MAD