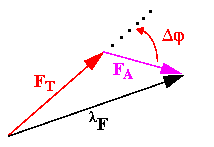
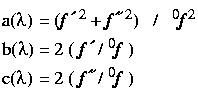
Now I'm going to simplify the notation a bit and rewrite the previous equation so that the variables we want to solve for more or less match the labels in our original diagram
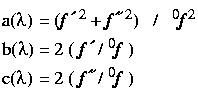
Each of our measurements of F(h) at some wavelength gives us one
instance of the equation above, and the separate instances may be
treated as a system of simultaneous equations from which we want to
obtain the quantities FA, FT, and
.
Actually we have two measurements for each wavelength, because the
observation for F-(h) may be treated as an observation of
F+(h) with the value of
inverted.
So to obtain values of our three unknowns we will
need at least three observations,
which is to say data collected at two wavelengths with distinct
scattering factors. Obviously it is better to be over-determined, so we
would prefer data collected at three or more wavelengths
.
Now as written above, the equations are not linear. To solve them in practice (or at least as in the code implemented in the MADLSQ program [Hendrickson, 1985]) we treat them instead as a set of linear equations in 4 unknowns:
)P2
+ b()P3
+ c()P4
and enforce the fundamental identity (sin2 + cos2 = 1) via the addition of a Lagrangian constraint:
We then substitute in to find the quantities we really want:
=
arctan(P4/P3).
The treatment of data collected from crystals with more than one type of
anomalous scattering atoms is exactly parallel, with the addition of two new
quantities to be estimated for each new scattering type k:
|FAk| and
k .
So for two anomalous scattering types we have 5 unknowns and we will
need data from a minimum of three wavelengths
(F+ and F- at each of 3 wavelengths = 6 observations
to derive 5 unknowns).
back to index
next topic