n
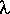= 2d sin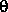
What is Bragg's Law and Why is it Important?
Bragg's Law refers to the simple equation:
(eq 1)
n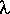 = 2d sin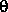
derived by the English physicists Sir W.H. Bragg and his son Sir W.L. Bragg in 1913 to
explain why the cleavage faces of crystals appear to reflect X-ray beams at certain angles
of incidence (theta, 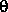). The variable d is the distance
between atomic layers in a crystal, and the variable lambda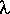
is the wavelength of the incident X-ray beam (see applet); n is an integer
This observation is an example of X-ray wave interference
(Roentgenstrahlinterferenzen), commonly known as X-ray diffraction (XRD), and was direct
evidence for the periodic atomic structure of crystals postulated for several centuries.
The Braggs were awarded the Nobel Prize in physics in 1915 for their work in determining
crystal structures beginning with NaCl, ZnS and diamond. Although Bragg's law was used to
explain the interference pattern of X-rays scattered by crystals, diffraction has been
developed to study the structure of all states of matter with any beam, e.g., ions,
electrons, neutrons, and protons, with a wavelength similar to the distance between the
atomic or molecular structures of interest.
How to Use this Applet
The applet shows two rays incident on two atomic layers of a crystal, e.g., atoms,
ions, and molecules, separated by the distance d. The layers look like rows because
the layers are projected onto two dimensions and your view is parallel to the layers. The
applet begins with the scattered rays in phase and interferring constructively. Bragg's
Law is satisfied and diffraction is occurring. The meter indicates how well the phases of
the two rays match. The small light on the meter is green when Bragg's equation is
satisfied and red when it is not satisfied.
The meter can be observed while the three variables in Bragg's are changed by clicking
on the scroll-bar arrows and by typing the values in the boxes. The d and
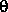variables can be changed by dragging on the arrows provided on the
crystal layers and scattered beam, respectively.
Deriving Bragg's Law
Bragg's Law can easily be derived by considering the conditions necessary to make the
phases of the beams coincide when the incident angle equals and reflecting angle. The rays
of the incident beam are always in phase and parallel up to the point at which the top
beam strikes the top layer at atom z (Fig. 1). The second beam continues to the next layer
where it is scattered by atom B. The second beam must travel the extra distance AB + BC if
the two beams are to continue traveling adjacent and parallel. This extra distance must be
an integral (n) multiple of the wavelength (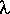) for the phases
of the two beams to be the same:
(eq 2)
n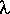 = AB +BC .
Fig. 1 Deriving Bragg's Law using the reflection geometry and applying trigonometry.
The lower beam must travel the extra distance (AB + BC) to continue traveling parallel and
adjacent to the top beam.
Recognizing d as the hypotenuse of the right triangle Abz, we can use trigonometry to
relate d and to the distance (AB + BC). The distance AB is
opposite so,
(eq 3)
AB = d sin .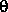
Because AB = BC eq. (2) becomes,
(eq 4)
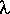n = 2AB
Substituting eq. (3) in eq. (4) we have,
(eq 1)
n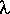 = 2 d sin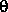
and Bragg's Law has been derived. The location of the surface does not change the
derivation of Bragg's Law.
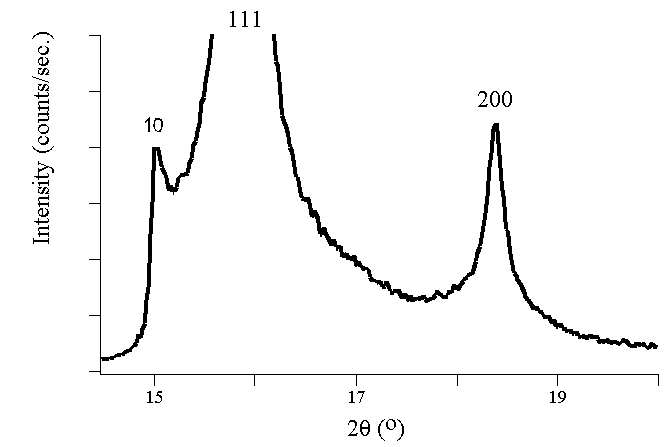
Experimental Diffraction Patterns
The following figures show experimental x-ray diffraction patterns of cubic SiC using
synchrotron radiation.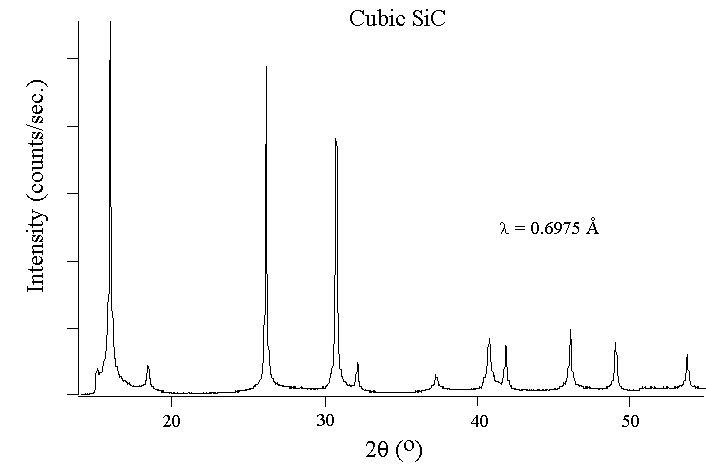 
Players in the Discovery of X-ray Diffraction
Friedrich and Knipping first observed Roentgenstrahlinterferenzen in 1912 after a hint
from their research advisor, Max von Laue, at the University of Munich. Bragg's Law
greatly simplified von Laue's description of X-ray interference. The Braggs used crystals
in the reflection geometry to analyze the intensity and wavelengths of X-rays (spectra)
generated by different materials. Their apparatus for characterizing X-ray spectra was the
Bragg spectrometer.
Laue knew that X-rays had wavelengths on the order of 1 Å. After learning that Paul
Ewald's optical theories had approximated the distance between atoms in a crystal by the
same length, Laue postulated that X-rays would diffract, by analogy to the diffraction of
light from small periodic scratches drawn on a solid surface (an optical diffraction
grating). In 1918 Ewald constructed a theory, in a form similar to his optical theory,
quantitatively explaining the fundamental physical interactions associated with XRD.
Elements of Ewald's eloquent theory continue to be useful for many applications in
physics.
Do We Have Diamonds?
If we use X-rays with a wavelength (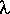) of 1.54Å, and we
have diamonds in the material we are testing, we will find peaks on our X-ray pattern at
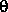values that correspond to each of the d-spacings that characterize
diamond. These d-spacings are 1.075Å, 1.261Å, and 2.06Å. To discover where to expect
peaks if diamond is present, you can set 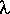to 1.54Å in the
applet, and set distance to one of the d-spacings. Then start with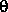
at 6 degrees, and vary it until you find a Bragg's condition. Do the same with each of the
remaining d-spacings. Remember that in the applet, you are varying ,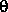
while on the X-ray pattern printout, the angles are given as 2.
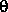Consequently, when the applet indicates a Bragg's condition at a particular angle, you
must multiply that angle by 2 to locate the angle on the X-ray pattern printout where you
would expect a peak.
|
Text written by Paul J. Schields Center for High Pressure Research Department of Earth & Space Sciences State University of New York at Stony Brook Stony Brook, NY 11794-2100. |
Applet created by Konstantin Lukin kostik_lukin@yahoo.com |
Project Java Webmaster Glenn A. Richard Center for High Pressure Research SUNY Stony Brook |
Applet updated by Jay Painter |
Mirrored from http://www.journey.sunysb.edu/ProjectJava/Bragg 3 Oct 2001
Last modified October 11, 2004