 ) for several wavelengths
) for several wavelengths
 i.
i.
The diagram below illustrates the vector relationships among three
quantities that we will estimate for each Bragg reflection h
by measuring the scattering amplitude
Fobs( ) for several wavelengths
) for several wavelengths
 i.
i.
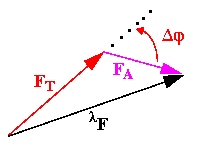
 = total observed scattering amplitude from our diffraction measurement
at wavelength
= total observed scattering amplitude from our diffraction measurement
at wavelength  ,
which has an unknown phase we would dearly like to know
,
which has an unknown phase we would dearly like to know
 = Difference in
phase angle between normal and anomalous scattering components
= Difference in
phase angle between normal and anomalous scattering components
The basic idea is that if we can locate the anomalous scattering atoms
within the unit cell (those contributing to FA) then we can
calculate the corresponding phase angle
 A.
The MAD phasing equations of
Karle [1980]
(which we will get to in a minute) can then be used to generate an estimate for
A.
The MAD phasing equations of
Karle [1980]
(which we will get to in a minute) can then be used to generate an estimate for
 and FT.
In the simplest case (we will later show more sophisticated estimates)
we can then estimate the phase of the FT as
and FT.
In the simplest case (we will later show more sophisticated estimates)
we can then estimate the phase of the FT as
 +
+
 A.
A Fourier transform of the amplitudes FT and phases
(
A.
A Fourier transform of the amplitudes FT and phases
( +
+
 A)
should yield an electron density map corresponding to all atoms in the
structure.
A)
should yield an electron density map corresponding to all atoms in the
structure.
We may further break down the anomalous scattering component into
contributions from several types of anomalous scatterers. Each anomalous
scattering type will have its own wavelength-dependent scattering
behaviour, which we will write:
 back to index
back to index
 next topic
next topic